[quote=“audioguy”]Thanks for the prompt & excellent reply! I have always been impressed by the service & help from Velleman.
I just tried what you suggested & it’s made it SO much easier to pick out the individual 2nd, 3rd, 4th harmonics.
May I just ask your advice, I have a 1kHz sine wave which is quite pure & has a THD of approx 0.001%, however when using the spectrum anaylser on the PCSU1000, while my calculations at this stage could also be questionable, the best I can calculate this to using the PCSU1000 is a THD of approx 0.3%.
In your experience, is it unrealistic to expect to be able to calculate a THD of around these kind of figures of 0.001% etc using the PCSU1000?[/quote]
It is an unrealistic expectation for the PCSU1000, and in fact for most digital 'scopes–here’s why.
To observe 0.001% distortion accurately would require the displayed amplitude of the highest harmonic to be at least 100 db below that of the primary frequency. However as most DSOs use 8-bit analog-to-digital converters (ADCs) their best case theoretical analog dynamic range is 48 dB, I.e. a measurement/noise floor of -48 dB.
Good news however is that when using the FFT function there is a noise floor improvement (NFI), that is a factor of the frequency resolution (FR) of the capture data, per this formula (this is what pushed your originally observed noise floor down to -60 dB):
Noise Floor Improvement (dB) = 10 * log10(FR) * k
where
[ul]FR is the reciprocal of the waveform capture time;
k is a factor (1 to as much as 3) dependent on the chosen windowing function;[/ul]
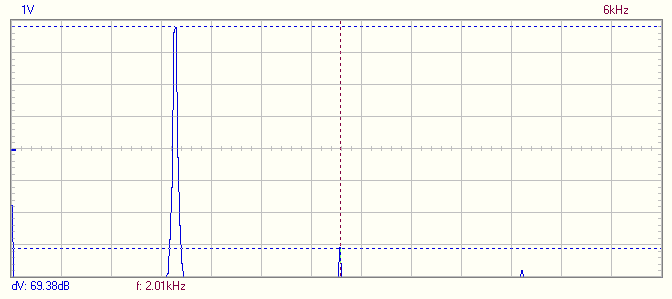
Based on the image posted by VEL225 I am guesstimating the frequency resolution to be 30 Hz or so (BTW, it would be neat if the FR could be displayed on the FFT screen), plugging that into the above formula and using a k of 1.0 we get:
NFI = 10 * log10(30) * 1.0 = 14.8 dB, making the total dynamic range 48.0 + 14.8 = 62.78 dB; making a positive harmonic amplitude observation limit of -55 dB, or 0.18 % at best.
Moving to a 12-bit scope would improve the analog dynamic range to 72.2 dB, however the NFI would remain the same for an FFT total dynamic range of 87 dB, still not enough for observing those -100 dB harmonics.
A 16-bit scope would do it. With a 96.3 dB base it’s FFT could muster a 111.0 db range and the 0.001% harmonics would be distinctly visible with appropriate window selection and averaging.